728x90

프림 알고리즘
- weight가 있는 undirected graph 에서 MST를 찾는 알고리즘
- 크루스칼 알고리즘 (krustal algorithm) 과 같은 용도. 상황에 따라 더 효율적인 알고리즘을 선택
작동 방식
- 임의의 vertex를 선택하여 Tree 생성 (현재 노드가 1개)
- T에 있는 노드와 T에 없는 노드 사이의 edge 중 weight가 최소인 edge를 찾는다
- 해당 edge가 연결하는 노드중, Tree에 없던 노드를 Tree에 추가
- 모든 노드가 Tree에 포함될 때까지 2-3을 반복
코드 구현
from math import inf
graph = [
[inf, 10, inf, 5, inf, inf, inf],
[10, inf, 2, 7, 12, inf, inf],
[inf, 2, inf, inf, 11, 14, inf],
[5, 7, inf, inf, 6, inf, 9 ],
[inf, 12, 11, 6, inf, 15, inf],
[inf, inf, 14, inf, 15, inf, 3 ],
[inf, inf, inf, 9, inf, 3, inf],
]
V, E = 7, 11
def prim(graph, V, E, start):
tree_node = set([start])
total_weight = 0
for _ in range(V - 1):
next_edge = (-1, -1, inf)
for node_from in tree_node:
for node_to in range(V):
if node_to not in tree_node:
if next_edge[0] == -1 or next_edge[2] > graph[node_from][node_to]:
next_edge = (node_from, node_to, graph[node_from][node_to])
total_weight += next_edge[2]
tree_node.add(next_edge[1])
return total_weight
result = prim(graph, V, E, 3)
print(result)
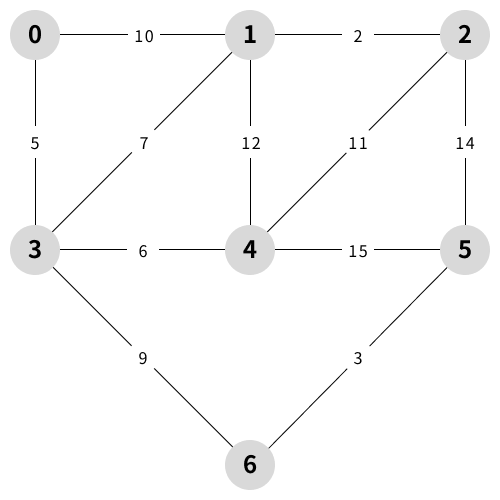
예시 설명
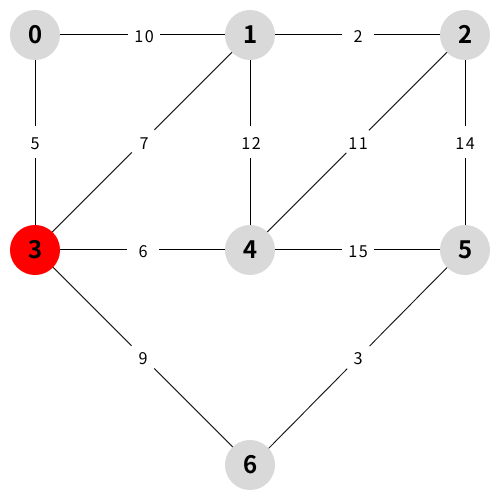
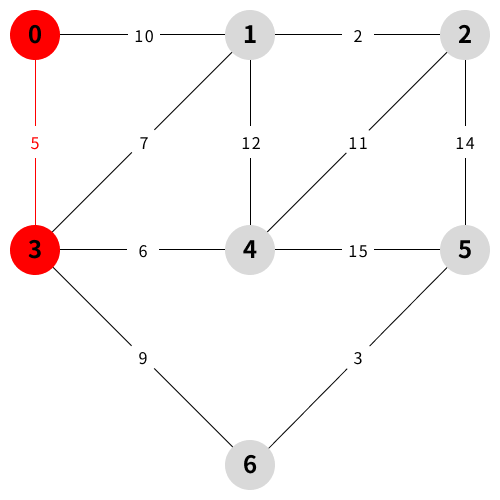
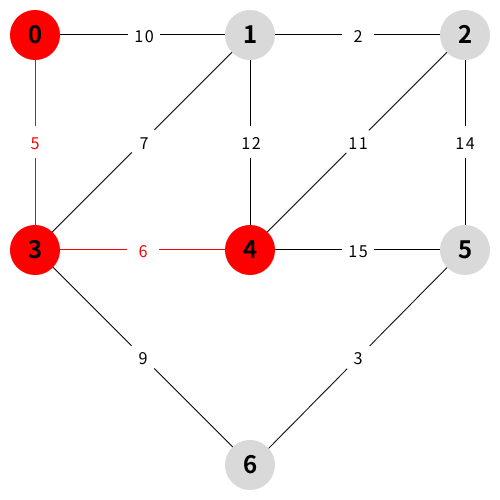
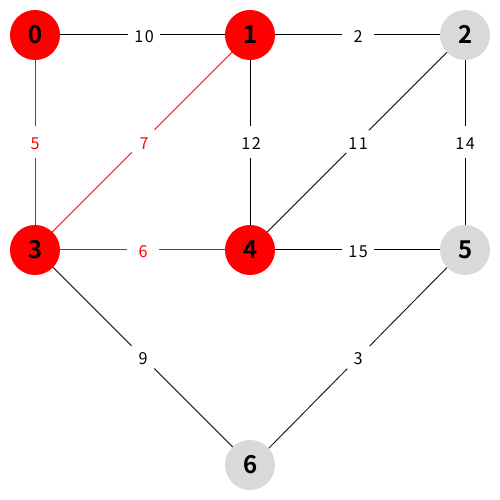
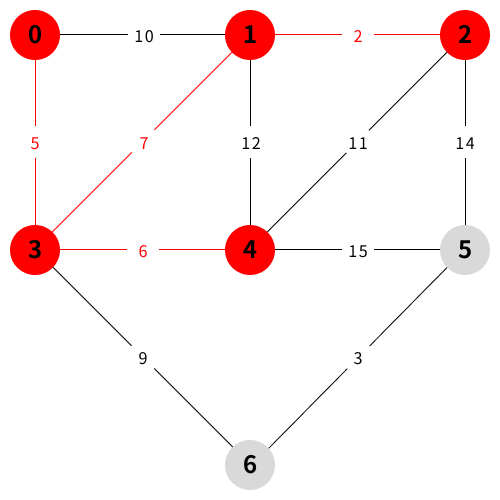
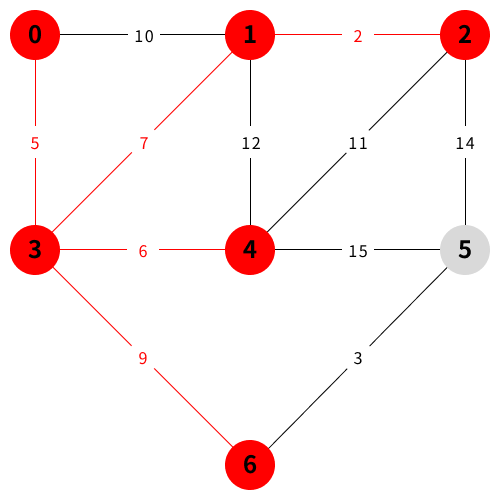
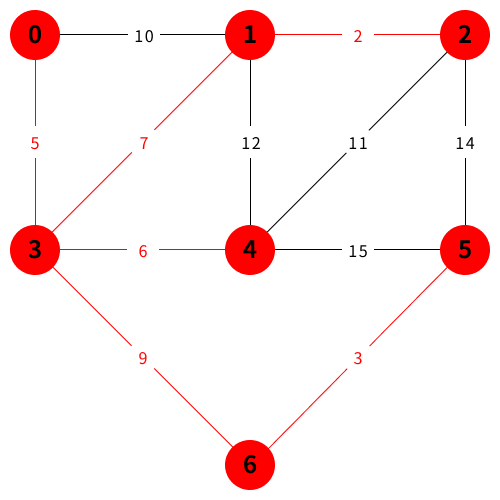
참조
- 위키백과
- ready2start 님의 블로그
- victolee 님의 블로그
반응형
'CS > Algorithm' 카테고리의 다른 글
| [알고리즘] Kruskal Algorithm(크루스칼 알고리즘) (0) | 2022.06.07 |
|---|---|
| [알고리즘] union-find Algorithm (0) | 2022.06.07 |

